Understanding Squeeze Theorem

In this short article, we’ll understand the squeeze theorem that comes in very handy for proving results in calculus and analysis. In fact, the Squeeze Theorem can also be used to prove the First Fundamental Theorem of Calculus.

Before going ahead, let us try to understand the need for it.

There are certain functions whose limit cannot be ascertained with normal limit laws. For e.g How can we evaluate

limx→0x2sin(1x)$$\underset{x\to 0}{lim}{x}^{2}sin(\frac{1}{x})$$

We know that limx→0sin(1x)$\underset{x\to 0}{lim}sin(\frac{1}{x})$ is not defined.

Hence, we cannot solve this by taking

limx→a(f(x).g(x))=limx→af(x).limx→ag(x)$$\underset{x\to a}{lim}(f(x).g(x))=\underset{x\to a}{lim}f(x).\underset{x\to a}{lim}g(x)$$

This is where the Squeeze Theorem comes in handy. It’s mathematically defined as follows: For

g(x)≤f(x)≤h(x) iflimx→ag(x)=limx→ah(x)=L thenlimx→af(x)=L$$g(x)\le f(x)\le h(x)if\underset{x\to a}{lim}g(x)=\underset{x\to a}{lim}h(x)=Lthen\underset{x\to a}{lim}f(x)=L$$

i.e. if f(x) is squeezed between g(x) and h(x) and its limit evaluates to the limits of g(x) and h(x).

The following figure represents the sin function squeezed between the quadratics:

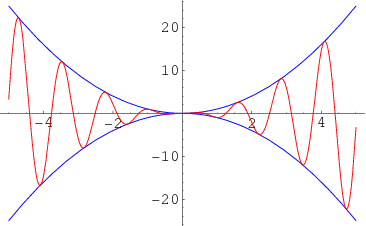
Image Source - Mathworld

Now, the sine function is defined as:

−1≤sin(1x)≤1$$-1\le sin\left(\frac{1}{x}\right)\le 1$$

So,

−x2≤x2sin(1x)≤x2$$-x^2\le x^{2}sin\left(\frac{1}{x}\right)\le x^2$$

As, limx→0−x2=limx→0x2=0$\underset{x\to 0}{lim}{-x}^2=\underset{x\to 0}{lim}{x}^2=0$ by applying the squeeze theorem, we get limx→0x2sin(1x)=0$\underset{x\to 0}{lim}{x}^{2}sin\left(\frac{1}{x}\right)=0$

Hence, we have evaluated the limit easily with the Squeeze theorem, which was otherwise not possible with normal limit laws.