Number System - Irrationals and Dedekind Cut

The first mathematical concept that a child is introduced to is the idea of numbers. Numbers have always fascinated the brightest minds and have always been the core part of mathematics. The whole concept of numbers might seem trivial initially, but the more mathematics you learn, the more you realise that numbers pose come from the most challenging problems in all of mathematics. We will take up several articles about these problems, but first begin with the number system. There are basically five main number systems - Natural Numbers, Integers, Rational Numbers, Real Numbers and Complex Numbers.

We will be taking up with the construction of Irrational Numbers and Real Numbers in this article. Let us first begin with formal definition of the other number systems. Natural numbers are used for counting and are also known as Positive Integers. They are more formally defined by Peano Axioms.

1. Zero is a number.
2. Given any natural number n there is another n+1 that comes next - known successor of n.
3. Zero is not the successor of any number.
4. Two numbers are equal if there successor are equal.

Natural numbers are closed under multiplication and addition but require large number system for subtraction and division. The set of all natural numbers is denoted by N.

Integers consist of natural number and the negatives of non-zero natural numbers and are denoted by Z. Integers are closed under the operations of addition, multiplication and subtraction, but not under division as the quotient of two integers need not be an integer. For example, 2/3 tales out of the realm of integers.

This takes us to Rational Numbers. Rational Numbers are of the form a/b, where both a and b are integers. Physical quantities like length, weight, temperature, velocity cannot be measured absolutely with whole numbers. Hence, rational numbers are quintessential for measurement. But apart from practical purposes, how can we justify the need of rational numbers in a more mathematical way?

In our discussion of other number systems, we observed that none of them is closed under all basic operations - i.e. , addition, multiplication,subtraction and division. Natural numbers are not closed under subtraction and division. However, introduction of negative numbers allows integers to be closed under subtraction but not under division. But introduction of fractional numbers allows rational numbers to be closed under division too. As Richard Courant puts it in "what is Mathematics?"-In the domain of rational numbers, the so-called rational operations- addition , subtraction, multiplication and division- may be performed without any restriction and will never lead out of this domain. Such a closed domain of numbers is called a Field. The concept of fields takes us into abstract algebra, which we will take up in another article.

There are still some numbers which cannot be expressed in the form a/b. Such numbers are known as Irrational number. A very common example of an irrational number is 2√$\sqrt{2}$. Informally speaking, irrational numbers are those numbers that cannot be expressed as terminating or repeating decimals. However, such a definition would not be acceptable to a mathematician and he will certainly ask for a more rigorous statement or a rigorous construction of irrational numbers. The first rigorous construction of irrational and real numbers was given by Dedekind in his classic work - Continuity and Irrational numbers, first published in 1872.

Let us begin with the geometrical interpretation of rational numbers.

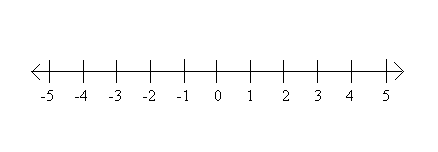
Figure 1 represents a number axis. To represent fractions with denominator n, we divide each of the segments of unit length into n equal parts; the points of subdivision then represent the fraction with denominator n. The points corresponding to rational numbers may be called Rational Points.

Dedekind extended this concept by showing that rational numbers satisfy a Trichotomy law, i.e., each rational 'm' divides the entire line into three parts - x itself, rational numbers greater than x and rational numbers less than x. There are, however, an infinite number on the line which are not rational points. Using the idea that every point on the line should correspond to a number, Dedekind introduced the concept of Cuts, which is portion of all rational numbers into two non-empty facts or classes- a lower class A and an upper class B, such that every number α$\alpha$ of the lower class is less than every number, β$\beta$ of the upper class.

Three different cases can arise:

1. The lower class can have a greatest number and the upper class no smallest number.
2. The upper class can have smallest number and the lower class no greatest number.

The first two cases describe all rational numbers.

1. The lower class can have no greatest number and the upper class no smallest number.

Let us try to understand this with the help of an example given in Clawson's book

*Let us arrange the positive integers and their squares in two given rows, so that the squares are underneath the numbers to which they correspond. Since the square of a fraction in its lowest terms is a fraction whose numerator and denominator are perfect squares, we see that there are not rational numbers whose squares are 2,3,4,5,6,8,10,11…… However, there are rational numbers whose squares are as near these numbers as we please. For instance the numbers

form an upper and a lower set in which the squares of the terms in the lower are less than 2, and the squares of the terms in the upper are greater than 2. We can find a number in the upper set and a number in the lower set such that their squares differ from 2 by a little as we please.

Now form a lower class, as described above, containing all negative rational numbers,zero and all positive rational numbers whose squares are less than 2; and an upper class containing all the positive rational numbers whose squares are greater than 2. the every rational number belongs to one class or the other. Also every number in the lower class is less than every number in the upper. The lower class has no greets number and the upper class has no smallest number.

When by any means we have obtained a division of all the rational numbers into two classes of this kind, the lower class having no greatest number and the upper class having no smallest number, we create a new number defined by this division. We call it an Irrational Number. *

A typical Dedekind cut of the rational number is given by:

A = {a ϵ$ϵ$ Q : a2$a^2$ < 2 ∨$\vee$ a ≤$\le$ 0}

B = {b ϵ$ϵ$ Q : b2$b^2$ > 2 ∨$\vee$ b > 0}